Thuật Toán Nén Huffman Tĩnh

THUẬT TOÁN NÉN HUFFMAN TĨNH

Data: ADDAABBCCBAAABBCCCBBBCDAADDEEAA

Số bit cần mã hóa: Len * 8 = 31 * 8 = 248 bit

I.       Lập bảng tần số:

Ký tự	Tần số
A	10
B	8
C	6
D	5
E	2

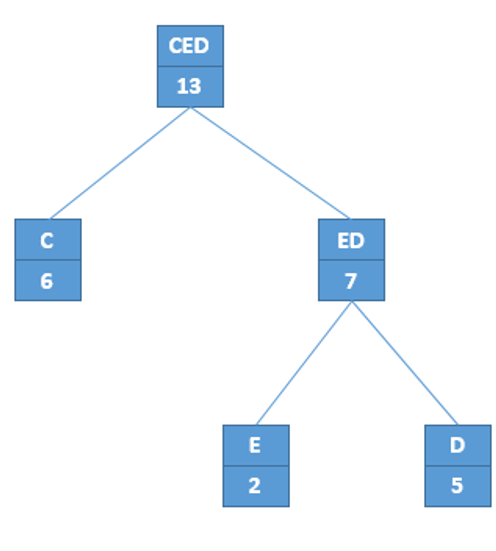
II.   Xây dựng cây:

Nhóm 2 chuỗi ký tự có tần số nhỏ nhất trước thành 1 chuỗi mới vì chuỗi ký tự được nhóm trước sẽ có đã dài mà Huffman dài hơn, chuỗi nhóm sau có độ dài mã Huffman ngắn hơn, nên chuỗi có tần số lớn nhất sẽ có mã Huffman ngắn nhất. Từ đó ta có chuỗi được nén được nén hiệu quả nhất.

Để tiện cho việc tạo cây ta có những quy ước sau:

·        Luôn nhóm 2 chuỗi ký tự có trọng số (tổng tần số các ký tự) nhỏ nhất.

·        Chuỗi có trọng số lớn hơn sẽ là nút phải

·        Nếu trọng số bằng nhau, chuỗi có ký tự nhỏ nhất lớn hơn sẽ là nút phải
 (VD: TCXB và KSAM thì TCXB là nút phải vì ‘C’ > ‘A’)

Chuỗi ký tự	Tần số
A	10
B	8
C	6
D	5
E	2

    Ø  E + D

Chuỗi ký tự	Tần số
A	10
B	8
ED	7
C	6

Ø  C + ED

Chuỗi ký tự	Tần số
CED	13
A	10
B	8

Ø  A + B

Chuỗi ký tự	Tần số
BA	18
CED	13

Ø  CED + BA

Chuỗi ký tự	Tần số
CEDBA	31

III.      Xây dựng bảng mã Huffman

Ta duyệt từ gốc đến ký tự, theo chiều duyệt cây cứ theo nút trái là 0, nút phải là 1 thì ta nhận được mã Huffman tương ứng với ký tự đó.

Ký tự	Mã Huffman
A	11
B	10
C	00
D	011
E	010

 

IV.       Nén chuỗi

Duyệt chuỗi Data, mỗi ký tự ta thay bằng mã Huffman

è Data nén: 110110111111101000001011111110100000001010100001111110110110100101111

Số bit mã hóa: 2 * 10 + 2 * 8 + 2 * 6 + 3 * 2 + 3 * 5 = 69

Hiệu suất nén: 1 – 69 / 248 * 100 = 72.18%

V.             Giải nén

Sau khi nén dữ liệu, dữ liệu được nén được lưu trữ hoặc gửi đến điểm đích và được giải nén để xem nội dung. Để giải nén được nội dung này thì dữ liệu đã nén phải luôn đi kèm với bảng mã Huffman, ta có thể xem bảng mã Huffman là chìa khóa để giải mã dữ liệu nén và mỗi dữ liệu nén sẽ có 1 bảng mã Huffman đặc trưng riêng.

Để giải được dữ liệu đã nén, ta duyệt chuỗi nhị phân theo cây được tạo bởi bảng mã huffman, ‘0’ để duyệt bên nhánh trái, ‘1’ để duyệt bên nhánh phải khi tới điểm nút lá ta có được ký tự tương ứng, sau đó ta trả về điểm gốc cây, và duyệt dữ liệu nén còn lại tương tự như trên.

CÁC PHÉP TOÁN TRÊN HỆ NHỊ PHÂN (32 BIT)

CÁC PHÉP TOÁN TRÊN HỆ NHỊ PHÂN (32 BIT)

          Các bạn lưu ý, mỗi phép toán nhị phân có thể có nhiều giải thuật khác nhau để áp dụng, nhưng để đơn giản mình xin trình bày những giải thuật đơn giản nhất, dễ cài đặt nhất.

          Do vấn đề thời gian, mình xin trình bày source code trước, chi tiết phân tích mình sẽ cập nhật sau.

PHÉP CỘNG

                    Trong 4 phép tính nhị phân, phép cộng được xem là phép cơ bản nhất mà những phép tính sau cần tới, các bạn sẽ hiểu rõ điều này sau khi đi qua tình phép tính.

Bạn có thể xem bài CỘNG NHỊ PHÂN BÀI PHÉP XOR

Ở đây mình xin giới thiệu một giải thuật đơn giản khác.

Code (C++)

void CongNhiPhan(int A[], int B[], int KQ[])

{

          int Nho = 0;

          int Tam = 0;

          for (int i = 32 - 1; i >= 0; i--)

          {

                    Tam = A[i] + B[i] + Nho;

                    KQ[i] = Tam % 2;

                    Nho = Tam >> 1;

          }

}

PHÉP TRỪ

          Bản chất phép trừ là phép cộng hay ta có thể hiểu như sau:

          A - B = A + (-B)

          Trong nhị phân (-B) chính là bù hai của B

          Vậy ta có A – B = A + BuHai(B);

PHÉP NHÂN

                    Trong 4 phép toán +, - , *, /, thì mức độ trừu tượng, phức tạp giải thuật cũng tăng dần.

Code (C++)

void NhanNhiPhan(int A[32],int B[32],int KQ[])

{

          int KQTam[32] = {};

          int TamA[32] = {};

          Gan(TamA, A); // gán TamA = A

          int K = 0;

          for(K = 0; K < 32; K++)

                    if(B[K] == 1)

                              break;

          for(int j = 31; j >= K; j--)

          {

                    if(B[j]==1)

                    {

                              cong(TamA, KQ, KQTam);

                              Gan(KQ, KQTam);// gán KQ = KQTam

                    }

                    DichTrai(TamA, 1);

          }

}

         

PHÉP CHIA

          Phép chia là 1 bài toán khá thú vị, mình xin để lại cho các bạn suy nghĩ, mình sẽ cập nhật phần này sau.

Ngựa Sông

MERGESORT

MERGESORT

MergeSort là một giải thuật hay, chia nhỏ dãy đầu vào,  sử dụng phương pháp trộn 2 dãy đã được sắp xếp. Ở đây mình xin giới thiệu source code kèm theo hướng dẫn.

CODE (C++)

void MergeSort(int A[], int L, int R)
          // *** Sắp xếp mảng A, gồm N phần tử bằng giải thuật MergeSort
          // *** Ý tưởng: Ta chia dãy số thành 2 dãy, sau trộn hai dãy này thành 1 dãy, dãy này là kết quả,
          //   hai dãy được chia phải được sắp xếp, để đảm bảo điều này,
          //      ta xem mỗi dãy là 1 dãy mới và cũng chia nhỏ như dãy ban đầu, đến khi dãy chia nhỏ đã sắp xếp
{
          if (L < R) // Nếu L == R, xem như dãy đầu vào có 1 phần tử, và dãy này đã được sắp xếp.
          {
                    int K = (L + R) / 2;
                    // Chia dãy đầu vào thành 2 dãy mới
                   MergeSort(A, L, K);
                   MergeSort(A, K + 1, R);
                  //Trộn hai dãy trên thành 1 dãy, trong đó trong đó vị trí phân cách giữa hai dãy
                  //                   ngầm định là K = (L + R) / 2
                  Merge(A, L, R);
          }
}

void Merge(int A[], int L ,int R)
          // *** Trộn hai dãy nằm kề nhau và được phân cách ngầm định là K = (L + R) / 2
          // *** Ý tưởng: Ta lần lượt duyệt các phần tử của cả hai dãy,
          //          ở mỗi lượt duyệt ta duyệt hai phần tử 1 của dãy I, 1 của dãy II
          //          so sánh 2 phần tử và lấy ra phần tử nhỏ hơn bỏ vào dãy Kết Quả,
          //          cứ như vậy 2 dãy được trộn với nhau
{
          // Vì trộn dãy không mang tính tự đổi chỗ, nên ta phải dùng một mảng trung gian,
          //          ở đây ta dùng mảng B là mảng chứa dãy cần trộn, A là mảng lưu dãy đã được trộn
          int B[MAXSL] = {};
          for (int u = L; u <= R; u++)
                    B[u] = A[u];

          int K = (L + R) / 2;
          int i = L;
          int j = K + 1;
          int t = L - 1;
          // Trộn hai dãy
          while (t < R)
          {
                    if ((B[i] <= B[j] || j == R + 1) && i != K + 1)
                    {
                              t++;
                              A[t] = B[i];
                              i++;
                    }
                    if ((B[i] > B[j] || i == K + 1) && j != R + 1)
                    {
                              t++;
                              A[t] = B[j];
                              j++;
                    }
          }
}

Các bạn có thể tải hoặc xem code tường minh hơn ở đây

Ngựa Sông

PHÉP CÔNG NHỊ PHÂN BẰNG PHÉP XOR

PHÉP CÔNG NHỊ PHÂN BẰNG PHÉP XOR

Chào mọi người! Hôm nay, mình xin giới thiệu giải thuật cộng 2 số nhị phân, lấy ý tưởng dựa trên các phép bit đơn giản (and, or, xor, not), cụ thể là phép XOR.

Phép XOR
Bảng chân trị:

Giá trị phép XOR bằng 0 khi cả hai chân trị đầu vào giống nhau, điều này đúng với N chân trị đầu vào có cùng chân trị, ví dụ: 0 xor 0 xor 0 ... xor 0 = 0, nhưng không đúng với 1 xor 0 xor 0 ... = ?

Bài toán phép cộng:
Khi ta cộng 2 số nhị phân, ta sẽ lần lượt cộng các số từ phải sang trái, dựa trên bản chân trị:

+ 0     1
0     0   1
1   1   10

Với 1 + 1 = 10 ta viết 0 và nhớ 1
Tức khi ký số KetQua[i] = A[i] + B[i] + Nho
nếu KetQua[i] >= 10 thì Nho = 1; KetQua[i] = KetQua[i] % 10; (%: chia lấy dư)
ngược lại Nho = 0;

Mối liên hệ giữa phép cộng Bit và Phép XOR

Ta có bản so sánh sau:

  Từ bản trên ta rút ra nhận xét:
KetQua[i] = A[i] xor B[i] xor Nho;
Nho = 1, nếu A[i] + B[i] + Nho > 1;
Nho = 0, ngược lại;

CODE (c++)

void Cong(bool A[], bool B[], bool KQ[])
{
  bool Nho = 0;
for (int i = SOBIT - 1; i > -1; i--)
{
KQ[i] = A[i] ^ B[i] ^ Nho; // Trong C++, phép XOR được ký hiệu là ^
if (A[i] + B[i] + Nho < 2)
Nho = 0;
else Nho = 1;
  }
}

Các bạn có thể xem code tường minh hơn ở đây.

Ngựa Sông